Below text is part of documentation of project named "Eagle". The main goal of the project is to invent, develop and construct entirely new type of propulsion engine capable to propel space vehicle regardless of environment.

Vehicle propelled by inertial system moving vertically in gravitational field is capable of achieving steady state of levitation that is weightlessness. This happens when gravity acceleration is counterbalanced by acceleration coming from engine. Engine's acceleration has to be the same value, the same direction but opposite turn. These days there are some machines capable of doing it for example all choppers, some fighting planes (British Harrier), lifter, and potentially rockets.
As stated above gravity acceleration has to be counterbalanced by engine's acceleration. Of course where is acceleration there is a force. Because the two accelerations regard the same body (vehicle), whole problem is reduced to two opposed forces equal in strength. Engine of levitating vehicle is to create force equal to force of gravity acting upon this vehicle.

Now there comes a question about energy requirements of such engine. There are two major obstacles in determining work done by vehicle's engine in gravity field. First, work in gravity field is assumed to be self-preserving. You must do some work on body (raise to higher level or in another words put away to bodies acting gravitationally) to derive work of that body back. Second, work in mechanics is calculated assuming that body is moving, propagating space! If there is no movement, there is no work done in physical sense. Such approach is contradictive to observation of levitating chopper. You can't stand that the chopper flies without any use of energy. It would have been a perpetum mobile device then. It certainly uses energy, a lot of energy despite of this simple equation defining work.

In this system, when body is not moving, that is d = 0, work W is always zero, too. One should approach the issue in another way. One has to eliminate the distance d from equation by substituting d with something else. The simplest solution to this problem is taking into consideration equation defining distance passed by moving body with acceleration a in time t. This is the equation. (e2)

In above equation a is a gravity acceleration g. Therefore equation takes following form:

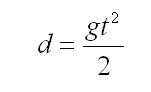
In the first equation e1 we see force F acting upon body with mass m. There is well known fundamental relation between accelerated body and acting force described as F = m * a. Ofcourse, in our case acceleration is gravitational one, so we've got:

Now we have all necessary compounds for substitution. We put it into equation e1 and get:

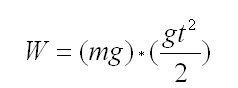
We put some order to it and get:

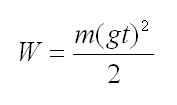
In this equation g is acceleration in meters per square power of second, It reduces to a meters per one second. The time is one second, so we could simplify equation ommiting t². We'll do it later. The above equation shows energy (work) required to be done by engine to cancel gravity and achieve levitation. The more time passes, the more energy we must spend. The second information we could obtain is power. As we know power is defined as work W done in time t. This is simple equation as this:

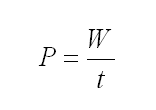
Now, we substitute into equation e7 for W with equation e6 and get:

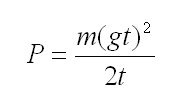
We have time t in numerator and denominator. We abbreviate equation for time and get:

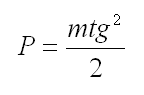
As we now, both power P and gravitational constant g is expressed per one second we can now assume that time t in this equation is also one second. We can simplify equation to the final form:

All we need to do is to substitute the right values to g and m to obtain final result. We know that:

m = 1 kg
g = 9.81 m/s²

We get:

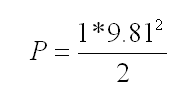
And final the result is:

It follows that for every 1 kilogramme of body mass in order to obtain levitation we have to provide 48.1 Watts that is 48.1 Joules in every second. It might look illusivelly small, but it isn't. In typical space modules with mass of 8 tons (nearly 13 thsd lbs) required power to lift off the ground is not less than 365 kW (365 thsd W). In reality required power is much higher, since electricity generators and engine have their own masses. Commercially available electric power generators providing required power weight at least two tons (3,3 thsd lbs). The propulsion system itself would weight also one tonne. Required power rises up to 510 kW. Though obtained result is much lower than systems use today. The ratio of the useful payload to mass of engine and fuel is far superior than today systems can reach. We can make aware oneself of to how great extent today systems are wasteful.
Using ideal system for entering the lower orbit for the vehicle with mentioned mass requires at least two times more power engine and generator (i.e. 1 MW) and total fuel usage ends up with 200 kg regular fuel like car gasoline (oxygen included). Consumption of energy sums up to 900 MJ (millions of Joules). Though it is much less than rockets use. In the course of several minutes similar rocket engine consumes 250 tones of fuel of total energy at least 3 x 10¹² Joules (trillions of Joules). It results in average power of 20 giga watts. In such conditions unmanned or manned orbital flights, not to mention about further trips are simply uneconomical daydream. The rockets are a dozen or so thousands times less energy efficient then ideal engine and much more expensive. You can realize that two small AA size NiMH cells - 2100 mAh each, could provide enough energy to launch into low orbit (180 km) a 1.5 kg device.